GROUPES (mathématiques) - Groupes finis

GROUPES (mathématiques) - Groupes finis

Née de l’étude des groupes de permutations des racines d’équations, la théorie des groupes finis s’est développée indépendamment depuis le Traité des substitutions et des équations algébriques (1870) de Camille Jordan. Après les travaux importants de Burnside, de Frobenius et de leurs élèves vers le commencement du XX^e siècle, cette théorie connut une période de développement lent, faute de méthodes pour résoudre les nombreux problèmes posés par ces pionniers. Les efforts de mathématiciens comme P. Hall et R. Brauer pendant cette période ont engendré les nouvelles méthodes qui, après 1955, ont amené une intense activité dans ce domaine; des progrès énormes ont été accomplis, particulièrement dans la théorie des groupes simples et la théorie des relations entre un groupe et ses sous-groupes. Mais beaucoup de questions sont restées longtemps ouvertes et sont l’objet d’une recherche acharnée.

1. Groupes de permutations

Historiquement la théorie des groupes finis commença avec l’étude des groupes symétriques et de leurs sous-groupes, les groupes de permutations. Soit E un ensemble fini formé des n éléments e ¹, ..., e ⁿ , n 閭 1. Une permutation 神 des éléments e ¹, ..., e ⁿ (ou encore une permutation 神 sur E) est une application x 料 神(x ) de E dans E, telle que chaque élément y de E soit l’image y = 神(x ) d’un élément unique x de E. L’application 神^-1, envoyant chaque élément y sur l’élément x tel que y = 神(x ), est alors aussi une permutation sur E, qui s’appelle l’inverse de 神. Le produit 神福 de deux permutations 神, 福 sur E est la permutation de e ¹, ..., e ⁿ définie par: 神福(x ) = 神( 福(x )), pour tout x dans E. Avec ces définitions de l’inversion et de la multiplication, l’ensemble des permutations sur E forme un groupe fini (E), le groupe symétrique de E. Son élément neutre est la permutation identité 1 = 1^E sur E, qui envoie chaque x = e ¹, ..., e ⁿ sur lui-même: 1^E(x ) = x .

Le groupe symétrique (E) est déterminé à un isomorphisme près par le nombre n = |E| d’éléments de E; et on l’appelle souvent le groupe symétrique ⁿ de degré n , sans spécifier l’ensemble E. L’ordre | ⁿ | du groupe ⁿ, c’est-à-dire le nombre de ses éléments, est n ! = 1.2... (n 漣 1).n .

On peut représenter une permutation 神 de e ¹, ..., e ⁿ graphiquement par un tableau formé des éléments e ¹, ..., e ⁿ et de flèches. Chaque flèche joint un élément x = e ¹, ..., e ⁿ à son image y = 神(x ). Par exemple, si 神 est la permutation des éléments a , b , c , d , définie par 神(a ) = c , 神(b ) = a , 神(c ) = d , 神(d ) = b , son tableau est:

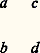Une permutation comme celle-ci, dont le tableau a la forme d’une seule boucle, s’appelle une permutation cyclique. Elle se note en donnant les éléments dans leur ordre cyclique 神 = (a , c , d , b ). Dans cette écriture, on peut commencer avec n’importe quel élément et écrire 神 sous les formes équivalentes:

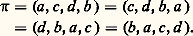Toute permutation sur E s’écrit comme un produit de permutations cycliques sur certains sous-ensembles de E. Ainsi, la permutation 神 de 1, 2, ..., 6 définie par: 神(1) = 5, 神(2) = 6, 神(3) = 3, 神(4) = 2, 神(5) = 1, 神(6) = 4, a pour tableau:

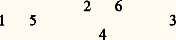Il est évident que l’ensemble1, 2, ..., 6 se décompose en une réunion disjointe des sous-ensembles1, 5,2, 6, 4 et3, sur lesquels 神 opère comme les permutations cycliques (1, 5) (2, 6, 4) et (3). Ces permutations cyliques sont les cycles de 神. La longueur d’un cycle de 神 est le nombre d’éléments dans le sous-ensemble correspondant. Donc 神 a des cycles de longueur 2, 3 et 1. On écrit 神 comme le produit (dans n’importe quel ordre) de ses cycles: 神 = (1, 5)(2, 6, 4) (3) = (4, 2, 6)(3)(1, 5) = ...

On a l’habitude de supprimer les cycles de longueur 1 quand l’ensemble E est connu. On écrit ainsi (1, 5)(2, 6, 4) au lieu de (1, 5)(2, 6, 4)(3) pour la permutation considérée précédemment. Cette notation est cohérente avec la notation adoptée pour la multiplication, car la permutation (1, 5)(2, 6, 4) = (1, 5)(2, 6, 4)(3) est en fait le produit des permutations (1, 5) = (1, 5)(2)(3)(4)(6) et (2, 6, 4) = (2, 6, 4)(1)(3)(5).

Si les longueurs des cycles d’une permutation 神 sont l ¹, ..., l ^k alors la signature sgn( 神) de 神 est le nombre:

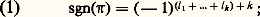donc la signature de (1, 5)(2, 6, 4) est (face=F0019 漣 1)^(2+3)+2 = 漣 1.

Si cette signature est égale à 1, la permutation 神 est paire , si elle est égale à 漣 1, elle est impaire. La fonction sgn est une fonction multiplicative : sgn( 神福) = sgn( 神)sgn( 福), pour toutes les permutations 神 et 福. L’application 神 料 sgn( 神) est donc un morphisme surjectif du groupe ⁿ sur le groupe multiplicatif des nombres 梁 1 (si n 閭 2). Le noyau de ce morphisme, c’est-à-dire l’ensemble Aⁿ , des permutations paires de ⁿ est alors un sous-groupe distingué de ⁿ . C’est le groupe alterné de degré n. Son ordre est |Aⁿ | = n !/2.

Les groupes ⁿ et Aⁿ sont des exemples de groupes de permutations. Un tel groupe G sur un ensemble E est un sous-groupe quelconque du groupe symétrique (E). Le degré , deg G, de G est alors le nombre |E| d’éléments dans E. Son ordre |G| est le nombre de ses éléments.

À chaque élément x de E on associe son stabilisateur G^x , le sous-groupe de toutes les permutations 神 dans G envoyant x sur lui-même: 神(x ) = x .

Si, pour tout couple (x , y ) d’éléments distincts de E, il existe au moins une permutation 神 dans G telle que 神(x ) = y , on dit que le groupe G est transitif. Par exemple, le groupe alterné Aⁿ est transitif pour n 閭 3: si x et y sont deux éléments distincts de E, il existe un élément z de E, distinct de x et de y. La permutation (x , y , z ) est paire, d’après (1), et envoie x sur y .

On a déjà décomposé une permutation 神 sur un ensemble E en permutations cycliques sur certains sous-ensembles disjoints de E. De manière analogue, on peut décomposer un groupe G de permutations sur E en groupes transitifs de permutations sur certains sous-ensembles disjoints de E. À tout élément x de E, on associe sa G-orbite G(x ), qui est l’ensemble de toutes les images 神(x ) de x par les permutations 神 de G. L’élément x = 1(x ) appartient à son orbite G(x ), et, pour tout élément y 捻 G(x ), on a G(y ) = G(x ). L’ensemble E est donc la réunion disjointe des G-orbites E¹, ..., E^k de ses éléments. Si une permutation 神 appartient à G, sa restriction 神ⁱ est une permutation sur l’orbite Eⁱ , pour i = 1, ..., k . Ces restrictions 神¹, ..., 神^k déterminent la permutation 神. L’ensemble Gⁱ des restrictions 神ⁱ (à Eⁱ ) des permutations 神 de G est un groupe transitif de permutations sur Eⁱ , i = 1, ..., k ; et l’application 神 料 神ⁱ est un morphisme surjectif du groupe G sur Gⁱ . On a donc analysé le groupe G en les groupes transitifs G¹, ..., G^k au moyen des morphismes 神 料 神ⁱ .

La famille des groupes transitifs de permutations est universelle , en ce sens que chaque groupe fini H est isomorphe à un groupe G de cette famille. En effet, chaque élément 靖 de H détermine une permutation 神 size=1^靖 des éléments de H, définie par 神 size=1^靖( 精) = 靖精, pour tout 精 de H. L’application 靖 料 神 size=1^靖 est un isomorphisme du groupe H sur un groupe transitif G de permutations sur H. Le groupe G ainsi obtenu a la propriété suivante: Si une permutation 神 de G laisse invariant au moins un élément de l’ensemble sur lequel G opère, alors 神 = 1. On appelle régulier tout groupe transitif de permutations ayant cette propriété. Tout groupe régulier G de permutations s’obtient à partir d’un groupe abstrait H de la manière décrite plus haut.

Comme la famille des groupes transitifs de permutations est universelle, il ne peut être question de les classer tous. On peut pourtant essayer de classer certaines sous-familles importantes de ces groupes. Une de ces sous-familles est celle des groupes de Frobenius. Un tel groupe G est un groupe transitif, mais non régulier, de permutations sur un ensemble E, avec la propriété suivante: Si une permutation 神 dans G laisse invariants au moins deux éléments de E, alors 神 = 1. Frobenius a montré (en 1901) qu’un groupe de Frobenius a toujours un unique sous-groupe régulier distingué K, appelé noyau de Frobenius de G, tel que G = G^x K et G^x 惡 K =1 pour tout stabilisateur G^x d’un élément x dans E. En 1936, Zassenhaus a donné une classification complète des stabilisateurs G^x des groupes de Frobenius. Il n’y a pas de classification complète des noyaux K de Frobenius, mais Thompson (1959) a démontré une conjecture de Frobenius: tous ces noyaux sont des groupes nilpotents.

Une autre sous-famille est la famille des groupes de Zassenhaus. Un groupe de Zassenhaus G est un groupe transitif de permutations sur un ensemble E, tel que la restriction d’un stabilisateur G^x soit un groupe de Frobenius sur l’ensemble formé de E moins l’élément x. Pour éviter les cas triviaux, on suppose aussi qu’il n’y a pas de sous-groupe régulier distingué dans G. Zassenhaus, Feit, Ito et Suzuki sont arrivés à une classification complète des groupes de Zassenhaus. Un tel groupe G est soit un PSL(2, K) pour un corps fini K (cf. infra , chap. 2), ou une extension de ce groupe par un groupe d’ordre 2, soit un des groupes de Suzuki (une autre famille de groupes simples découverte par Suzuki en 1960 lors de l’étude de ce problème).

Un groupe G de permutations sur un ensemble E est n-fois transitif , pour un entier positif n , si |E| 閭 n , et si, chaque fois que l’on considère deux n -chaînes x ¹, ..., x ⁿ et y ¹, ..., y ⁿ d’éléments de E où les x ¹, ..., x ⁿ (resp. y ¹, ..., y ⁿ ) sont tous distincts, il existe au moins une permutation 神 dans G, telle que 神(x ¹) = y ¹, ..., 神(x ⁿ ) = y ⁿ . Les groupes de Zassenhaus sont des groupes 2-fois transitifs. Le groupe symétrique ⁿ est n -fois transitif, pour tout n 閭 1. Le groupe alterné Aⁿ est (n 漣 2)-fois transitif pour n 閭 3. Il y a beaucoup de groupes 3-fois transitifs, les groupes PGL(2, K), par exemple, où K est un corps fini. Mais on ne connaît que quatre groupes 4-fois transitifs, autres que les groupes ⁿ pour n 閭 4, et Aⁿ pour n 閭 6. Ce sont les groupes de Mathieu (1861 et 1873) M²⁴, M²³, M¹², M¹¹, dont les degrés et les ordres sont: deg (M²⁴) = 24, avec |M²⁴| = 244 823 040; deg (M²³) = 23, avec |M²³| = 10 200 960; deg (M¹²) = 12, avec |M¹²| = 95 040; deg (M¹¹) = 11, avec |M¹¹| = 7 920. Les groupes M²⁴ et M¹² sont même 5-fois transitifs, mais non 6-fois transitifs. On a de bonnes raisons de croire que tout groupe 6-fois transitif (ou plus) est ⁿ ou Aⁿ , mais il n’y a aucune démonstration de cette conjecture.

2. Groupes simples

Si H est un sous-groupe distingué d’un groupe fini G, le morphisme surjectif naturel de G sur le groupe quotient G/H, ayant H pour noyau, nous donne une sorte d’analyse du groupe G en les deux groupes H et G/H. Les deux cas H =1, et H = G sont triviaux, le groupe G étant alors isomorphe à l’un des deux groupes H et G/H. Dans tous les autres cas, les ordres |G/H| et |H| sont strictement plus petits que l’ordre de G. Les groupes G/H et H sont donc plus simples que G. Le groupe G est appelé simple si G 1 et si l’on ne peut pas l’analyser ainsi en des groupes d’ordre strictement plus petit, c’est-à-dire si1 et G sont les seuls sous-groupes distingués de G. Par exemple, pour chaque entier premier p , le groupe cyclique C^p d’ordre p est simple.

Tout groupe fini G peut se décomposer en groupes simples: si G =1, il n’y a rien à faire; si G 1, il y a toujours un sous-groupe distingué H¹ de G tel que G/H¹ soit un groupe simple. Si H¹ =1, l’analyse est terminée. Sinon, il existe un sous-groupe distingué H² de H¹, tel que H¹/H² soit un groupe simple. Si on itère cette construction, on aboutit à une suite G = H⁰, H¹, H², ..., Hⁿ =1 de sous-groupes de G, où Hⁱ est distingué dans H^i-1 , et où H^i-1 /Hⁱ est un groupe simple, i = 1, ..., n . Une telle suite s’appelle une suite de Jordan-Hölder du groupe fini G, et les groupes quotients H⁰/H¹, H¹/H², ..., H^n-1 /Hⁿ : s’appellent les facteurs de Jordan-Hölder de G. La terminologie adoptée ici suit N. Bourbaki; les théoriciens des groupes finis, traditionnellement, continuent à réserver le terme de suite de composition à ce que nous appelons ici suite de Jordan-Hölder.

Considérons, par exemple, le groupe symétrique ⁴ des permutations de 1, 2, 3, 4. L’ordre de ⁴ est 4! = 24. Le groupe alterné A⁴ d’ordre 4!/2 = 12 est un sous-groupe distingué dans ⁴, et le groupe quotient ⁴/A⁴ est isomorphe au groupe simple C². Les trois permutations (12)(34), (13)(24), (14)(23) forment avec l’identité un sous-groupe V d’ordre 4 dans A⁴ qui s’appelle le 4-groupe de Klein. Ce groupe V est distingué dans ⁴, et donc dans A⁴. Le groupe quotient A⁴/V est isomorphe au groupe C³. Le 4-groupe V est commutatif, et tous ses sous-groupes sont distingués. Pour 靖 = (12)(34), ou 靖 = (13)(24), ou 靖 = (14)(23), le sous-groupe 靖, 1 est isomorphe à C², ainsi que le groupe quotient V/ 靖, 1. On a donc construit pour ⁴ une suite de Jordan-Hölder ⁴, A⁴, V, 靖, 1,1, ayant comme facteurs de Jordan-Hölder C², C³, C², C² (à des isomorphismes près).

Un groupe fini dont chaque facteur de Jordan-Hölder est isomorphe à un C^p , où p est un nombre premier, est dit résoluble. Le groupe ⁴ est donc résoluble.

Dans l’exemple ci-dessus, il y avait trois choix possibles pour le groupe 靖, 1. Un groupe G peut donc avoir plusieurs suites de Jordan-Hölder. Il y a malgré tout une certaine unicité des suites de Jordan-Hölder: les facteurs de Jordan-Hölder de G sont indépendants du choix de la suite de Jordan-Hölder (théorème de Jordan-Hölder ), c’est-à-dire que, si G = H⁰, H¹, ..., Hⁿ =1, et G = K⁰, K¹, ..., K^m =1 sont deux suites de Jordan-Hölder de G, on a n = m , et il existe une permutation 神 de1, ..., m = n telle que le groupe H^i-1 /Hⁱ soit isomorphe au groupe K size=1^{神(i )} size=1^漣1/K size=1^{神(i )}, pour tout i = 1, ..., m = n. Chaque groupe fini peut donc être analysé en groupes simples uniques, qui sont ses facteurs de Jordan-Hölder. D’où l’importance de l’étude des groupes simples.

Les premiers groupes simples non cycliques furent découverts dans la première moitié du XIX^e siècle. Les groupes alternés Aⁿ sont des groupes simples, pour tout n 閭 5. C’est sur cette découverte que repose la démonstration moderne du théorème suivant d’Abel (1824): Les équations de degré 5 ne sont pas résolubles au moyen des seules opérations d’addition, de soustraction, de multiplication, de division et d’extraction des racines n -ièmes effectuées sur leurs coefficients.

Puis, en étudiant les groupes linéaires sur un corps fini K, on découvrit d’autres groupes simples. Pour chaque entier n 閭 1, les n 憐 n matrices (a ^ij ) à coefficients a ^ij dans K, et de déterminant det (a ^ij ) non nul, forment un groupe GL(n ,K) pour la multiplication (a ^ij ) (b ^ij ) = (c ^ij ) où:

avec i = j = 1, ..., n.

Le groupe GL(n ,K) s’appelle le groupe linéaire général de degré n sur K. L’application (a ^ij ) 料 det(a ^ij ) est un morphisme surjectif du groupe GL(n ,K) sur le groupe multiplicatif du corps K. Le noyau SL(n , K) de ce morphisme surjectif est donc un sous-groupe distingué de GL(n , K). Le centre Z de GL(n , K), formé des matrices de la forme xI , où I est la matrice identité et x un élément non nul de K, est aussi un sous-groupe distingué. Le groupe quotient GL(n , K)/Z se note par PGL(n , K), et l’image SL(n , K)Z/Z de SL(n , K) dans ce groupe par PSL(n , K). Jordan et Dickson ont montré que, si n 閭 3, ou si n = 2 et si K a plus de trois éléments, le groupe PSL(n , K) est simple; c’est le seul facteur de Jordan-Hölder de GL(n , K) qui soit simple et non cyclique.

La théorie des groupes linéaires généraux a été étendue aux autres groupes classiques par Jordan, Dickson et d’autres, vers la fin du XIX^e siècle. Pour chaque groupe linéaire général, orthogonal, symplectique ou unitaire, ils trouvèrent un ou plusieurs groupes correspondants (cela pour tout corps fini K). À quelques exceptions près (elles sont en nombre fini), tous ces groupes ont la propriété du groupe GL(n , K); ils ont un et un seul facteur de Jordan-Hölder qui soit simple et non cyclique.

Les groupes simples définis par les groupes classiques sont eux-mêmes des cas spéciaux des groupes simples de Lie. En plus de ces groupes, il y a cinq groupes de Lie simples exceptionnels. Dickson découvrit des groupes finis correspondant à certains de ces groupes exceptionnels, mais c’est Chevalley, en 1955, qui donna une méthode générale de construction des groupes finis simples, correspondant à n’importe quel groupe simple de Lie (cf. GROUPES - Groupes de Lie). Il découvrit ainsi de nouveaux groupes finis simples, correspondant aux autres groupes de Lie exceptionnels. Steinberg (1959) compléta le travail de Chevalley en construisant des variantes de ces groupes. Pour cela, il s’est inspiré de la construction des groupes unitaires comme des variantes des groupes linéaires généraux.

En 1959, la liste des groupes finis simples qui étaient connus contenait les groupes alternés Aⁿ , les groupes de Chevalley, leurs variantes de Steinberg et cinq groupes isolés: les quatre groupes M¹¹, M¹², M²³, M²⁴ de Mathieu et le stabilisateur d’un élément de M²³, qui s’appelle le groupe M²² de Mathieu. Les groupes de Mathieu mis à part, tous ces groupes appartenaient à de bonnes familles infinies.

Cet ordre relatif fut ébranlé par Suzuki, qui découvrit, en étudiant les groupes de Zassenhaus, une nouvelle famille infinie de groupes simples de permutations. Mais Rhee s’aperçut bientôt, en 1961, que l’on pouvait construire ces groupes de Suzuki avec une nouvelle variante de la construction de Chevalley, variante possible seulement pour certains corps finis. En appliquant cette méthode à d’autres groupes simples de Lie, Rhee trouva deux nouvelles familles infinies de groupes finis simples. Les groupes de Suzuki et de Rhee n’étant que des variantes des groupes de Chevalley, tout rentra dans l’ordre.

L’ordre ne dura pas longtemps. En classant les groupes finis simples possédant des 2-sous-groupes de Sylow abéliens, Janko (1966) découvrit un nouveau groupe simple isolé d’ordre 175 560. Depuis lors, de nombreux autres groupes finis simples, apparaissant comme isolés et exceptionnels (d’où leur nom de «groupes sporadiques») ont été découverts: le nombre de ces groupes sporadiques, incluant les groupes de Mathieu, était de vingt-six en 1980.

Il est nécessaire ici de préciser ce que l’on entend par «découverte» d’un groupe fini simple sporadique. En effet, l’existence de nombre de ces groupes a souvent été prédite avant d’être effectivement prouvée, la prédiction se fondant sur des coïncidences numériques ou structurelles que le hasard seul ne pouvait raisonnablement expliquer. On peut noter l’analogie de cette démarche scientifique avec certains aspects de l’histoire de la théorie des particules élémentaires. C’est ainsi que Janko a prédit en 1974 l’existence du quatrième des groupes sporadiques qui porte son nom, mais qu’il a fallu attendre 1980 pour qu’une construction effective de ce groupe soit menée à bien à l’université de Cambridge, à l’aide de nombreuses heures de calcul sur ordinateur.

Le plus «gros» des groupes sporadiques est celui que l’on a dénommé le «monstre», dont l’existence a été prédite en 1973 par B. Fischer et R. Griess; son nombre d’éléments est de l’ordre de 10⁵⁴. Malgré l’énormité de ce nombre, il semble pourtant que l’existence des groupes sporadiques traduise le phénomène souvent rencontré que certaines propriétés des nombres entiers ne sont vraies qu’à partir d’une certaine valeur: les petits nombres sont souvent exceptionnels. De fait, le plus grand nombre premier divisant le nombre d’éléments d’un groupe sporadique est 71 (en l’occurrence, 71 divise l’ordre du monstre). L’existence des groupes sporadiques semble également liée aux coïncidences ou isomorphismes exceptionnels entre «petits» groupes classiques.

Les spécialistes ont annoncé en 1980 que la classification des groupes finis simples était achevée, et par conséquent que les seuls groupes finis simples sont les groupes cycliques d’ordre premier, les groupes alternés de degré supérieur à 5, les groupes classiques et leurs variantes construits par Chevalley et ses successeurs (groupes appelés désormais «groupes de type de Lie»), et enfin les vingt-six groupes sporadiques connus. Le nombre de pages imprimées consacrées au travail de classification des groupes finis simples est de l’ordre de 10 000; les démonstrations s’appuient très souvent les unes sur les autres, et sont en général très complexes. Aucun mathématicien n’est en mesure, aujourd’hui, de vérifier tout seul cette gigantesque démonstration ou d’en comprendre les mécanismes profonds, et certains spécialistes pensent donc que, dans son état actuel, elle n’est pas tout à fait convaincante. Il est à noter que cette démonstration ne fournit aucune preuve a priori de l’existence d’un nombre fini de groupes sporadiques. Ce n’est qu’a posteriori, une fois la classification établie, que l’on constate que tel est bien le cas.

Le principe de la démonstration est celui de la récurrence: considérant un groupe G dont tous les facteurs de Jordan-Hölder de tous les sous-groupes propres sont isomorphes à l’un des groupes «connus», on essaye de démontrer que G est lui-même isomorphe à un groupe connu. L’outil essentiel de cette démarche est l’étude des centralisateurs d’involutions, qui repose sur deux résultats fondamentaux. Le premier est dû à R. Brauer, et affirme qu’il n’y a qu’un nombre fini de groupes finis possédant une involution (c’est-à-dire un élément de carré l’identité) dont le centralisateur (c’est-à-dire l’ensemble des éléments du groupe qui commutent avec cette involution) soit isomorphe à un groupe fixé.

Le deuxième, dont la démonstration est l’une des plus difficiles de l’histoire des mathématiques, est dû à W. Feit et J. G. Thompson (1963); il affirme que tous les groupes finis et simples sont d’ordre pair, à l’exception des groupes cycliques C^p d’ordre premier p. Ce remarquable théorème a été une conjecture «impossible» pendant plus de cinquante ans. Il est à la base de plusieurs travaux qui cherchent à classer certaines sous-familles de groupes simples distingués par les propriétés de leurs sous-groupes. Par exemple, les groupes finis simples dont les 2-sous-groupes de Sylow sont dièdres furent classés par Gorenstein et Walter (1965). De tous les théorèmes de classification, le plus important et le plus difficile est le théorème de Thompson (1966) pour les groupes simples minimaux , c’est-à-dire pour les groupes finis simples G tels que chaque sous-groupe H G soit résoluble. Cette classification a déjà permis de démontrer plusieurs conjectures anciennes, ainsi que de nouveaux théorèmes.

L’un des aspects les plus mystérieux de la théorie des groupes finis est le phénomène baptisé moonshine par J. H. Conway. Il s’agit d’une correspondance extraordinaire entre le monstre et la théorie des fonctions automorphes, correspondance constatée mais à ce jour totalement inexpliquée. Il existe une série formelle: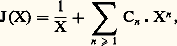

à coefficients dans l’anneau des caractères du monstre, possédant la propriété suivante: pour tout élément g du monstre, la fonction j (g ) définie sur le demi-plan de Poincaré 流 =z 捻 C/Im z 礪 0 par:

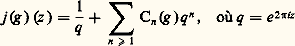est une fonction remarquable; plus précisément, il existe un sous-groupe discret 臨(g ) de GL²(Q) tel que la surface 流/ 臨(g ) se compactifie en une surface de genre 0, et toutes les fonctions modulaires pour 臨(g ) s’expriment rationnellement en j (g ). La fonction j (1) est, à une constante près, l’invariant modulaire j .

3. p-groupes

Si H est un sous-groupe d’un groupe fini G, son ordre |H|, son indice [G: H] (c’est-à-dire le nombre de classes à gauche de H dans G) et l’ordre |G| de G sont liés par le théorème de Lagrange (1770):

En particulier, |H| divise |G|. Soit p un nombre premier et p ⁿ la plus grande puissance de p qui divise |G|. Tout p-sous-groupe H de G (c’est-à-dire tout sous-groupe dont l’ordre |H| est une puissance p ^k de p ) a un ordre |H| 諒 p ⁿ . Si |H| = p ⁿ , on dit que H est un p-sous-groupe de Sylow de G. Il y a plusieurs théorèmes de Sylow (1872) pour ces sous-groupes:

1. Tout groupe fini G a au moins un p -sous-groupe de Sylow P.

2. Tout autre p -sous-groupe de Sylow Q de G est un conjugué de P, c’est-à-dire que Q = 靖P 靖^-1, pour un élément 靖 de G.

3. Tout p -sous-groupe H de G est un conjugué d’un sous-groupe de P, c’est-à-dire que 精H 精^-1 說 P, pour un élément 精 de G.

4. Le nombre l des p -sous-groupes de Sylow de P divise |G| et est de la forme l = 1 + pm , pour un certain entier m.

Le deuxième de ces théorèmes implique que le p -sous-groupe de Sylow P est déterminé, à un isomorphisme près, par le groupe G. On peut donc classer les groupes finis suivant leurs p -sous-groupes de Sylow; d’où l’importance de la théorie des p -groupes (groupes P dont l’ordre est une puissance p ^k 礪 1 d’un nombre premier p ). L’une des propriétés de ces groupes est que leurs centres Z(P) sont toujours non triviaux , soit Z(P) 1. Chaque p-groupe P est donc nilpotent (cf. GROUPES - Généralités, fin du chap. 3).

Si G est un groupe fini et si E est un sous-ensemble de G, le normalisateur ^G(E) de E dans G est le sous-groupe formé des éléments 靖 de G, tels que 靖E 靖^-1 = E. On montre alors qu’un groupe fini G est nilpotent si et seulement si tout sous-groupe H de G, différent de G, est strictement contenu dans son normalisateur ^G(H). On peut aussi montrer qu’un groupe fini G est nilpotent si et seulement si G n’a qu’un p -sous-groupe de Sylow G^p pour chaque nombre premier p. Dans ce cas, G est le produit direct de ses uniques sous-groupes de Sylow G^p . Les groupes finis nilpotents sont donc «presque» des p -groupes.

Plusieurs théorèmes relient la structure des normalisateurs ^G(H) des p -sous-groupes H 1 d’un groupe fini G avec celle de G. Frobenius a, par exemple, donné un critère pour la p-nilpotence de G, c’est-à-dire pour l’existence d’un sous-groupe distingué K dans G tel que P 惡 K =1 et PK = G pour tout p -sous-groupe de Sylow P. Voici le critère: un groupe fini G est p-nilpotent si le normalisateur ^G(H) est p-nilpotent pour tout p-sous-groupe H 1 de G. Notons qu’en général ces normalisateurs ^G(H) sont plus petits que G (par exemple, si G est simple et non cyclique).

Certains travaux récents de Thompson ont montré qu’il n’est pas nécessaire de vérifier la p -nilpotence de ^G(H) pour tout p -sous-groupe H de G. Il suffit d’en choisir quelques-uns qui soient significatifs. Le plus important de ses résultats est le suivant: Soit P 1 un p -sous-groupe de Sylow de G, et soit s le maximum des ordres |S| des sous-groupes commutatifs S de P. L’intersection A des sous-groupes commutatifs S de P, ayant pour ordre |S| = s , est un sous-groupe non trivial et distingué de P. Thompson a montré que le groupe G est p-nilpotent si ^G(A) l’est et si p 閭 3. Il suffit donc de regarder le normalisateur du seul p -sous-groupe A de G.

Il y a d’autres généralisations du théorème de Frobenius à des théorèmes sur l’existence de p -groupes quotients du groupe G sous certaines conditions sur les normalisateurs des p -sous-groupes de G. Les résultats de ce type jouent un rôle important dans l’étude des groupes simples et, en particulier, dans le théorème de Feit et Thompson.

Encyclopédie Universelle. 2012.